Se comenta que
la resolución de un sistema lineal de inecuaciones se le atribuye a Joseph
Fourier, después de quien nace el método de eliminación de Fourier-Motzkin. Posteriormente,
la programación lineal se plantea como un modelo matemático desarrollado
durante la Segunda Guerra Mundial para planificar los gastos y los retornos, a
fin de reducir los costos al ejército y aumentar las pérdidas del enemigo;
adicionalmente se utilizaba para la distribución de comida y municiones para
sus batallones, entre otros. Este método se mantuvo en secreto hasta 1947. En
la postguerra, muchas industrias lo usaron para optimizar el uso de materiales
de fabricación de productos para aumentar sus ganancias y minimizar sus costos.
Lo esencial de este tipo de ejercicios es
que podemos llevar problemas de la vida real a lenguaje matemático (modelado),
y posteriormente optimizarlo para obtener su mayor rendimiento con los métodos
que nos ofrece la investigación de operaciones.
En esta oportunidad, nos centraremos en aquellos problemas simples de programación lineal, los que tienen solamente 2 variables, manejados en el plano llamados comúnmente como “método gráfico”. Según el autor Hamdy Taha, en su libro “Investigación de Operaciones” lo señala como problemas bidimensionales con solución gráfica. Lo fundamental en estos
problemas de optimización, es definir los tres componentes básicos:
- Variables de decisión: son aquellas que definen el comportamiento del problema. Ejemplo: X1: Cantidad de producto Z a comprar para producir Y.
- Objetivo: que a nivel de estudio y así denominado por el autor Hamdy Taha “Función Objetivo”; aquí se debe definir si la función es maximizar o minimizar. Ejemplo: Z=A.X1+B.X2, donde según sea el caso podría ser maximizar las ganancias, minimizar los costos.
- Restricciones: permitirán definir y acotar el problema, estos son (regularmente) inecuaciones. Ejemplo: X1+ X2<20, lo que significa que la suma de las variables X1 y X2 sea menor a 20.
Posteriormente de haber definido estos tres componentes se procede a graficar en el plano y se acota según indiquen las restricciones para encontrar la región factible del problema, en esta área todos los puntos son soluciones que cumplen con las restricciones pero solo uno o más puntos son los puntos óptimos o “Soluciones Óptimas” que dan respuesta a ser el o los puntos máximos o mínimos de la función objetiva. Hay también la posibilidad de que no haya solución óptima y puede ocurrir por dos razones:
1. Que no haya región acotada o que no todas las restricciones se acoten. Ejemplo:
Veamos el siguiente ejemplo
sencillo.
Ejemplo 1: Una línea de viaje en tren ofrece asientos para
fumadores a un precio de Bs 1.000 y para no fumadores a un precio de Bs 600.
Por otra parte, a los no fumadores se les deja llevar un máximo de 50Kg en
equipaje y los fumadores 20Kg, la capacidad máxima del tren en equipaje es de
3.000Kg. Si el tren tiene 90 asientos, ¿Cuál debe ser la oferta de asientos
para cada tipo de pasajeros, con la finalidad de optimizar su ganancia?
Respuesta: Definimos los componentes básicos para resolver
el problema:
Variables de decisión:
Función Objetivo:
Como se desea obtener el mayor beneficio
es un problema de Maximizar:
Restricciones: Sacaremos restricción por restricción según el enunciado:
Restricciones: Sacaremos restricción por restricción según el enunciado:
A) “…a los no
fumadores se les deja llevar un máximo de 50Kg
en equipaje y los fumadores 20Kg, la capacidad máxima del tren en equipaje es
de 3.000Kg”
B) “…el tren tiene 90 asientos…” es
decir, que la cantidad de asientos para fumadores y no fumadores debe ser menor
o igual a 90 asientos.
C) Por último se definen las restricciones
lógicas, en este caso nos podemos preguntar ¿Es posible que
o
den valores negativos? En otras palabras,
¿Estaría bien decir un resultado como: - 40 asientos para no fumadores y -20
para fumadores? Por supuestos que no, cuando contamos asientos lo hacemos de
manera positiva, por tanto definimos:
Recomendación: para graficar es
preferible despejar una de las variables al a un lado de la desigualdad, y
tratar a una variable como “X” y la otra como “Y” para que se nos muestre más
sencillo al momento de graficar, en este caso se tomará a X1 como “X” y X2
Una vez obtenida la región factible
ubicaremos todos los vértices y estos valores serán evaluados en la función
objetivo.
Vértice (0,60):
Z(0,60)=1000x0+600x60= Bs. 36.000
Vértice (50,40):
Z(50,40)=1000x50+600x40= Bs. 74.000
Vértice (90,0): Z(90,0)=1000x90+600x0=Bs. 90.000
Vértice Optimo
Solución:
La oferta de asientos para que haya un mayor beneficio ha de ser 90 asientos
para fumadores, para obtener una ganancia máxima de Bs. 90.000
En
este sencillo ejemplo se muestra la aplicabilidad del método gráfico de manera
detallada. Más adelante, en una próxima entrega se presentará un ejemplo con
mayor cantidad de restricciones y por ende mayor cantidad de vértices para
evaluar. 







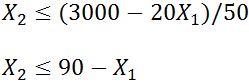








Este comentario ha sido eliminado por el autor.
ResponderEliminarHola Leonardo,
ResponderEliminarFelicidades por tu blog, me gustó mucho la cantidad y calidad de información relevante y variada, además de lo dinámico que es. La única recomendación es que a la página principal, en donde se encuentran los meses, esas letras colocarlas un poco más visibles.
Muchas gracias por compartir tan valiosa información.
Gracias por tu aporte Yikcy, me contenta que este contenido te fue de utilidad. Saludos
Eliminar